Category: science

PAUL Orienteering

ruminator

This is an example of a technique for orienteering.
A few days ago a video rotated onto my YouTube feed. It was a sample of field exercises taught by the Pathfinder School. One that caught my attention was the Positive Azimuth Uniform Layout method for orienteering. When I saw them working out the solution back to camp on the ground, I immediately recognized a graphical solution to the coordinate problem that surveyors used to solve all the time (before GPS surveying).

The approach is based on the conversion of bearing (or azimuth) and distance to northing and easting coordinates. When I learned to survey (with a 20-second transit, a 100-foot steel tape, a dumpy level, and a three-section level rod) this was how we did the calculations. Therefore, I wondered if I could use a slide rule to do the trigonometry, squares, and square roots required to obtain an arithmetic solution. The figure is the result of that with one error — I forgot to convert the angle (from the east-west axis) to a bearing (from the north-south axis). The error is corrected in the figure.

I also ran the solution with a hand calculator. (I used an HP-35s for the vector addition.) The calculations can be done with a pencil, piece of paper, and a slide rule. I used a Versalog 1461 (six-inch version of the Versalog slide rule). The solution is plenty good enough to return to camp.

That was fun.

Mars Insight Landing

ruminator1 Comment
I watched the final few minutes of the Insight landing. It was successful.

Decades ago I often rose early to watch launches of probes from Cape Canaveral. I recall watching video from the Apollo missions to the moon. I ate these events up, being fascinated by science and astronomy since I was very young.

I never imagined that I would watch the scientists and engineers at Jet Propulsion Laboratory working on the landing of a geophysical probe on Mars — on my computer over the Internet. Yet, today at noon, I did just that. I watched the control room at JPL as they monitored the probe's entry of the Mars atmosphere and touchdown on the surface.

I am still a little astounded by this. I never expected it.

The probe is important. If the science is successful, it will gather data about the interior of Mars. It will be our first look at the interior of another planet.

I have lived through an incredible series of events. I do not remember it, but Sputnik flew when I was young. I watched the Mercury missions, then the Gemini missions, then the Apollo missions, and the Shuttle missions. I have stepped out my back door and watched the International Space Station fly overhead, a bright, fast-moving star.

These are incredible things. I am so grateful to have been a witness to these events. I am fascinated by all of God's creation, but space is the most fascinating of it all. The vastness of it boggles and expands the mind. Sometimes I think I have just a little insight into infinity. Sometimes…

Something Not Quite Right

ruminator
Is this failure of design or failure of implementation?

After the flooding from last winter, I have walked past this little detention pond a number of times. Each time I pause and wonder whether this was a design failure or an implementation failure.

They built a very nice rip-rap lined spillway along the left side of this image. However, when the pond filled and overflowed, the discharge passed along the left side of the sidewalk. Until recently, when it was repaired, there was a large rill that was scoured by the flow.

When I pass, I pause and shake my head a bit. I’m really glad this isn’t a large reservoir. That would be catastrophic.

Estimating Distance

ruminator

A couple of weeks ago, I was watching a football game with my family. It was near sunset and the sky was illuminated by the last rays of the setting sun. Far overhead, jetliners could be seen crossing the sky, their contrails bright and warm although I knew that they existed in deadly cold.

One of them was not at cruising altitude. Older Grandson asked “How high is that plane?”

“About 25,000 feet,” SiL responded. I thought it was closer to 10K AGL.

“I don’t think so; I think it’s closer to 10,000.”

A short debate ensued and it was interesting. I respect SiL’s opinion given he works with aircraft as a professional.

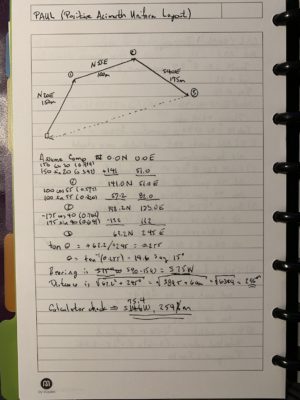
Later, on the road Monday, the interchange recurred to me. As I drove along, I wondered whether there was a simple way to estimate the altitude. After thinking about it a few minutes, I came up with the following.

For small angles, the angle and the sine of the angle are approximately equal. Therefore the angle subtended by the aircraft can be used to estimate its distance from the observer. If the approximate angle from the horizontal is also known, then the elevation can be estimated.

The width of a human thumb at arm’s length is about a half-degree, or thirty minutes of angle. The pinky fingertip is about half that.

As I thought about my observations, my estimate was about three of the aircraft would be the width of my pinky finger at arm’s length… or maybe half that. That would be between two and a half and five minutes of angle, or one-twelfth to one-twenty-fourth of a degree. The sight distance to the aircraft would then be 12 to 24 times the apparent width of the vehicle.

My guess is that the apparent width of that aircraft was on the order of 120–200 feet. Therefore, for S&G’s, say it was 150 feet. At twenty times the apparent width, that would be 30,000  feet. My estimate for the angle-to-horizon was less than 45 degrees, so I’ll use that as an upper limit. The sine of 45 is about 0.7. So, the elevation is about 70 percent of the length of the hypotenuse — or sight distance.

My estimate of the altitude of the aircraft is about 20,000 feet. SiL was closer to correct than I was. Trust the professional.

LaTeX?

ruminator

Apparently, WordPress has a \LaTeX interface for producing mathematics and math-like symbols. If it does, then this is something I’ve wanted in my weblog for a long time.

Alright, it works. The background is white and the foreground is black (duh), so it doesn’t quite work with my current color scheme, but it will do. At least I can now produce a decent-looking equation.